Question

A manufacturer of chocolate candies uses machines to package candies as they move along a filling line. Although the packages are labeled as 8​ ounces, the company wants the packages to contain a mean of 8.17 ounces so that virtually none of the packages contain less than 8 ounces. A sample of 50 packages is selected​ periodically, and the packaging process is stopped if there is evidence that the mean amount packaged is different from 8.17 ounces. Suppose that in a particular sample of 50 packages, the mean amount dispensed is 8.171 ​ounces, with a sample standard deviation of 0.052 ounce.1. Is there evidence that the population mean amount is different from 8.17 ounces? (Use a 0.01level of​ significance.)2. State the null and alternative hypotheses.H0​:μ ( ≥, ≤, =, <, >,≠ ) ________H1​:μ ( ≥, ≤, =, <, >,≠ ) ________​(Type integers or​ decimals.)3. The critical​ value(s) is(are) _____​(Round to four decimal places as needed. Use a comma to separate answers as​ needed.)4. The test statistic is _______​(Round to four decimal places as​ needed.)5. Reject/ Do not reject H0. There is sufficient/insufficient evidence to conclude the population mean amount is different from 8.17ounces.6. The​ p-value is _______​(Round to four decimal places as​ needed.)7. Interpret the meaning of the​ p-value. Choose the correct answer below.A. The​ p-value is the probability of obtaining a sample mean that is equal to or more extreme than 0.001 ounce below 8.17if the null hypothesis is false.B. The​ p-value is the probability of obtaining a sample mean that is equal to or more extreme than 0.001 ounce away from8.17 if the null hypothesis is true.A. The​ p-value is the probability of obtaining a sample mean that is equal to or more extreme than 0.001ounce aboveB. The​ p-value is the probability of not rejecting the null hypothesis when it is false.

Answer 1

We conclude that the mean amount packaged is equal to 8.17 ounces.

Explanation:

We are given that in a particular sample of 50 packages, the mean amount dispensed is 8.171 ​ounces, with a sample standard deviation of 0.052 ounces.

Let
`\mu` = population mean amount packaged.

So, Null Hypothesis,
`H_0` :
`\mu` = 8.17 ounces {means that the mean amount packaged is equal to 8.17 ounces}

Alternate Hypothesis,
`H_A` :
`\mu\\eq` 8.17 ounces {means that the mean amount packaged is different from 8.17 ounces}

The test statistics that will be used here is One-sample t-test statistics because we don't know about the population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean amount dispensed = 8.171 ounces

s = sample standard deviation = 0.052 ounces

n = sample of packages = 50

So, the test statistics =
`(8.171-8.17)/((0.052)/(√(50) ) )` ~
`t_4_9`

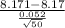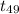
= 0.1359

The value of t-test statistics is 0.1359.

Also, the P-value of test-statistics is given by;

the meaning of the​ p-value is that the p-value is the probability of obtaining a sample mean that is equal to or more extreme than 0.001 ounces away from8.17 if the null hypothesis is true.

P-value = P(
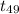`t_4_9` > 0.136) = More than 40% {from the t-table}

Since the P-value of our test statistics is more than the level of significance of 0.01, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region.

Therefore, we conclude that the mean amount packaged is equal to 8.17 ounces.