Answer:
2 -

Explanation:
Using the addition formula for tangent
tan(A - B) =
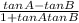 and the exact values
and the exact values
tan45° = 1 , tan60° =
 , then
, then
tan15° = tan(60 - 45)°
tan(60 - 45)°
=
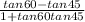
=
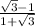
Rationalise the denominator by multiplying numerator/ denominator by the conjugate of the denominator.
The conjugate of 1 +
 is 1 -
is 1 -

=
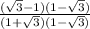 ← expand numerator/denominator using FOIL
← expand numerator/denominator using FOIL
=
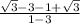
=
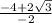
=
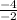 +
+
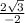
= 2 -
