Question

Doland is currently driving his car at 10 m/s. He sees Gooby and accelerates at 20 m/s2 for 2 seconds until he passes him to scare

him. How far did Doland drive during that time.

Answer 1

`60\; \rm m`.

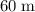Step-by-step explanation:

Refer to the velocity-time diagram attached. The displacement of an object over a period of time is equal to the area of the region between the velocity-time plot and the horizontal time axis. That is the case even if the velocity of the object is changing over time.

For the car in this question, the distance travelled in that two seconds should be equal to the trapezoid highlighted in green. That's the region bounded with:

• on the top: the velocity-time function of this car,
• on the two sides: the start and end of the acceleration (
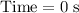  `\text{Time} = 0\; \rm s` and
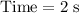  `\text{Time} = 2\; \rm s`,) as well as
• on the bottom: the horizontal time axis.

The formula for the area of a trapezoid is:

`\displaystyle \text{Trapezoid Area} = (1)/(2)* \text{Height} * (\text{Upper Base} + \text{Lower base})`.

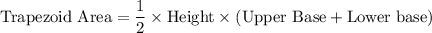For the imaginary trapezoid on this velocity-time graph:

• Height:
  `\text{Time taken} = 2\; \rm s`.
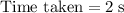• Upper base and lower base:
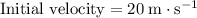  `\text{Initial velocity} = 20\; \rm m \cdot s^(-1)` and
  `\text{Final velocity} = 20\; \rm m \cdot s^(-1) + 2\; \rm s * 20\; \rm m \cdot s^(-1) = 50\; \rm m \cdot s^(-1)`.

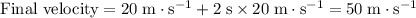Therefore:

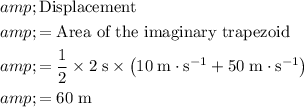`\begin{aligned}&\text{Displacement} \\ &= \text{Area of the imaginary trapezoid}\\ &= (1)/(2) * 2\; \rm s * \left(10\; \rm m \cdot s^(-1) + 50\; \rm m \cdot s^(-1)\right)\\ &= 60\; \rm m\end{aligned}`.