Question

Las edades de dos hermanos tienen una razón de 2 a 1. Cuando transcurran 4 años, la razón entre sus edades será de 8 a 6. ¿Cuántos años tienen actualmente?

Answer 1

The age of brothers are 4 years and 2 years respectively.

Explanation:

We are given that the ages of two brothers have a ratio of 2 to 1. When 4 years have passed, the ratio of their ages will be 8 to 6.

Let the age of the first brother be 'x years' and the age of the second brother be 'y years'.

So, according to the question;

• The first condition states that the ages of two brothers have a ratio of 2 to 1, that means;

`(x)/(y) =(2)/(1)`

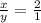
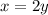`x=2y` -------------- [equation 1]

• The second condition states that when 4 years have passed, the ratio of their ages will be 8 to 6, that means;

`(x+4)/(y+4)=(8)/(6)`

`6({x+4})=8}(y+4)`

`6x+24=8y+32`

`6(2y)+24=8y+32`

`12y-8y=32-24`

`4y=8`

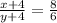
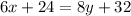
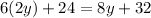
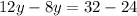
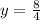`y=(8)/(4)` = 2 years

Putting the value of y in equation 1 we get;

x = 2y

x =
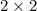`2 * 2` = 4 years

Hence, the age of brothers are 4 years and 2 years respectively.