Question

Ship A and Ship B are 120 km apart when they pick up a distress call from another boat. Ship B estimates that they are 70 km away from the distress call. They also notice that the angle between the line from ship B to ship A and the line from ship A to the distress call is 28°. What are the two possible distances, to the nearest TENTH of a km, from ship A to the boat?

Answer 1

The two possible distances from Ship A to the distress call boat are 64.4 km and 147.5 km

Explanation:

The given parameters are;

The distance between Ship A and Ship B = 120 km

The distance of the distress call from Ship B = 70 km

The angle made between the line from Ship A to B and the line from Ship A to the distress call = 28° = Opposite angle to the line from the location of the distress caller to Ship B

Therefore;

70/(sin(28°)) = 120/(sin(x))

Where;

x = The angle opposite the line from Ship A to B

sin(x) = ((sin(28°))×120)/70 = 0.805

x = sin⁻¹(0.805) = 53.59°

Therefore, the angle opposite the line from Ship A to the distress caller, r = 180 - (28 + 53.59) = 98.4°

From sin rule, we have;

70/(sin(28°)) = r/(sin(98.4°))

r = (70/(sin(28°)))×(sin(98.4°)) = 147.5

However by cosine rule, we have;

70² = 120² + r² - 2×120×r × cos(28°)

4,900 = 14,400 + r² - 211.907·r

r² - 211.907·r + 14,400 - 4,900 = 0

r² - 211.907·r + 9,500 = 0

Factorizing, we have;

`x = \frac{-b\pm \sqrt{b^(2)-4\cdot a\cdot c}}{2\cdot a}`

`r = \frac{211.907\pm \sqrt{211.907^(2)-4* 1* 9,500}}{2* 1}`

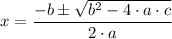
r = 64.406 km or 147.501 km

Which gives;

The distance of the line from Ship A to the distress caller = 64.4 km or 147.5 km to the nearest tenth.

The two possible distances from Ship A to the distress call boat = 64.4 km and 147.5 km