Question

If ABCD is an A4 sheet and BCPO is the square, prove that △OCD is an isosceles triangle. And find the angles marked as 1 to 8 without using a protractor

Answer 1

The diagram for the question is missing, but I found an appropriate diagram fo the question:

Proof:

since OC = CD = 297mm Therefore, Δ OCD is an isoscless triangle

∠BCO = 45°

∠BOC = 45°

∠PCO = 45°

∠POC = 45°

∠DOP = 22.5°

∠PDO = 67.5°

∠ADO = 22.5°

∠AOD = 67.5°

Explanation:

Given:

AB = CD = 297 mm

AD = BC = 210 mm

BCPO is a square

∴ BC = OP = CP = OB = 210mm

Solving for OC

OCB is a right anlgled triangle

using Pythagoras theorem

(Hypotenuse)² = Sum of square of the other two sides

(OC)² = (OB)² + (BC)²

(OC)² = 210² + 210²

(OC)² = 44100 + 44100

OC = √(88200

OC = 296.98 = 297

OC = 297mm

An isosceless tringle is a triangle that has two equal sides

Therefore for △OCD

CD = OC = 297mm; Hence, △OCD is an isosceless triangle.

The marked angles are not given in the diagram, but I am assuming it is all the angles other than the 90° angles

Since BC = OB = 210mm

∠BCO = ∠BOC

since sum of angles in a triangle = 180°

∠BCO + ∠BOC + 90 = 180

(∠BCO + ∠BOC) = 180 - 90

(∠BCO + ∠BOC) = 90°

since ∠BCO = ∠BOC

∴ ∠BCO = ∠BOC = 90/2 = 45

∴ ∠BCO = 45°

∠BOC = 45°

∠PCO = 45°

∠POC = 45°

For ΔOPD

`Tan\ \theta = (opposite)/(adjacent)\\ Tan\ (\angle DOP) = (87)/(210) \\(\angle DOP) = Tan^-1(0.414)\\(\angle DOP) = 22.5 ^(\circ)`

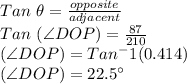
Note that DP = 297 - 210 = 87mm

∠PDO + ∠DOP + 90 = 180

∠PDO + 22.5 + 90 = 180

∠PDO = 180 - 90 - 22.5

∠PDO = 67.5°

∠ADO = 22.5° (alternate to ∠DOP)

∠AOD = 67.5° (Alternate to ∠PDO)