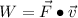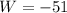Answer:
(a)
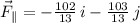 , (b)
, (b)
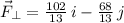 , (c)
, (c)
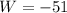
Step-by-step explanation:
The statement is incomplete:
The force on an object is
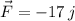 . For the vector
. For the vector
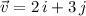 . Find: (a) The component of
. Find: (a) The component of
 parallel to
parallel to
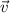 , (b) The component of
, (b) The component of
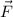 perpendicular to
perpendicular to
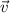 , and (c) The work
, and (c) The work
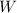 , done by force
, done by force
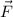 through displacement
through displacement
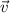 .
.
(a) The component of
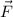 parallel to
parallel to
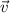 is determined by the following expression:
is determined by the following expression:
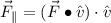
Where
 is the unit vector of
is the unit vector of
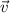 , which is determined by the following expression:
, which is determined by the following expression:

Where
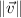 is the norm of
is the norm of
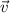 , whose value can be found by Pythagorean Theorem.
, whose value can be found by Pythagorean Theorem.
Then, if
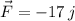 and
and
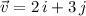 , then:
, then:
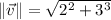
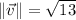
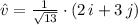
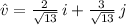
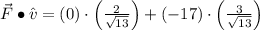
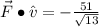
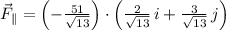
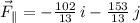
(b) Parallel and perpendicular components are orthogonal to each other and the perpendicular component can be found by using the following vectorial subtraction:
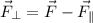
Given that
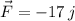 and
and
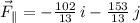 , the component of
, the component of
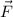 perpendicular to
perpendicular to
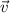 is:
is:
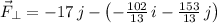

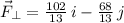
(c) The work done by
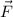 through displacement
through displacement
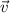 is:
is: