Question

AB is dilated by a scale factor of 3 to form A1B1. Point O, which lies on AB, is the center of dilation. The slope of AB is 3. The slope of A1B1 is . Through point O.

Answer 1

3, Does not Pass

Explanation:

Good luck with edmentum everyone :D

Answer 2

`Slope\ of\ A'B'= 3`

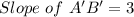
Explanation:

Given

`Slope\ of\ AB= 3`

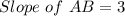
Required

Determine the slope of A'B'

Represent the coordinates of AB with (x,y), such that

`AB = (x,y)`

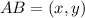
Since A'B' is 3 * AB, we have

`A'B' = 3 * AB`

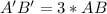
Substitute (x,y) for AB

`A'B' = 3 * (x,y)`

`A'B' = (3x,3y)`

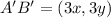
Since the slope of AB = 3, then the slope of A'B' is also equal to 3 because dilation through (0,0) does not have effect on the slope