Question

The equation for a parabola has the form y=ax2+bx+c, where a, b, and c are constants and a≠0. Find an equation for the parabola that passes through the points (−1,8), (2,−4), and (−6,−12).

Answer 1

The equation for the parabola that passes through the points (−1,8), (2,−4), and (−6,−12) is
`y = -x^(2)-3\cdot x +6`.

Explanation:

Let be (−1,8), (2,−4), and (−6,−12) points contained in a parabola, which is represented by a second-order polynomial. To determine the constant of the second-order polynomial, the following system of equations must be solved:

`a - b+c = 8`

`4\cdot a +2\cdot b +c = -4`

`36\cdot a -6\cdot b +c = -12`

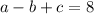
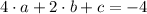
There are several methods for solving this: Equalization, Elimination, Substitution, Determinant and Matrix. The solution of this system is:
`a = -1`,
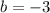`b = -3` and
`c = 6`. Hence, the equation for the parabola that passes through the points (−1,8), (2,−4), and (−6,−12) is
`y = -x^(2)-3\cdot x +6`.