Answer:
The unit vector in component form is
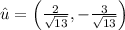 or
or
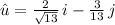 .
.
Explanation:
Let be
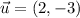 , its unit vector is determined by following expression:
, its unit vector is determined by following expression:
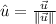
Where
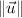 is the norm of
is the norm of
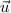 , which is found by Pythagorean Theorem:
, which is found by Pythagorean Theorem:

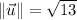
Then, the unit vector is:
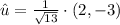
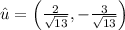
The unit vector in component form is
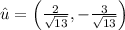 or
or
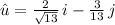 .
.