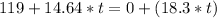Answer:
The time taken is

Step-by-step explanation:
From the question we are told that
The speed of first car is

The speed of second car is

The initial distance of separation is
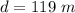
The distance covered by first car is mathematically represented as
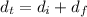
Here
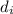 is the initial distance which is 0 m/s
is the initial distance which is 0 m/s
and
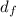 is the final distance covered which is evaluated as
is the final distance covered which is evaluated as
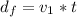
So
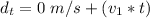
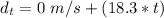
The distance covered by second car is mathematically represented as
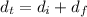
Here
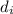 is the initial distance which is 119 m
is the initial distance which is 119 m
and
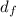 is the final distance covered which is evaluated as
is the final distance covered which is evaluated as
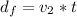
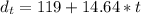
Given that the two car are now in the same position we have that