Question

Una bala de cañón se dispara horizontalmente con una velocidad inicial de 120m/s y un ángulo de elevación de 35°.Encuentra:a)su alcance maximo,b)si altura máxima,c)si tiempo maximo de vuelo

Answer 1

a) x = 1353,2 m.

b)
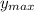`y_(max)` = 236,9 m [/tex]

c)
`t_(v) = 13,8 s`

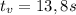
Step-by-step explanation:

a) El alcance máximo se puede calcular usando la siguiente ecuación:

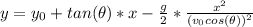`y = y_(0) + tan(\theta)*x - (g)/(2)*(x^(2))/((v_(0)cos(\theta))^(2))` (1)

En donde:

y: es la altura final = 0

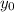`y_(0)`: es la altura inicial = 0

x: es el alcance

θ: es el angulo respecto a la horizontal = 35°

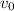`v_(0)`: es la velocidad inicial = 120 m/s

g: es la gravedad = 10 m/s²

Resolviendo la ecuación (1) para x, tenemos:

`x = (2tan(\theta)*(v_(0)cos(\theta))^(2))/(g) = (2tan(35)*(120 m/s*cos(35))^(2))/(10 m/s^(2)) = 1353,2 m`

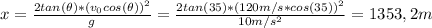
El alcance máximo es 1353,2 m.

b) La altura máxima es:

`y_(max) = (v_(0)_(y)^(2))/(2g) = ((v_(0)sen(\theta))^(2))/(2g) = ((120 m/s*sen(35))^(2))/(2*10 m/s^(2)) = 236,9 m`

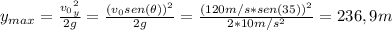
Entonces, la altura máxima es 236,9 m.

c) El tiempo de vuelo es el siguiente:

`t_(v) = (x)/(v_(0)cos(\theta)) = (1353,2 m)/(120 m/s*cos(35)) = 13,8 s`

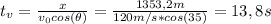
Por lo tanto, el tiempo de vuelo es 13,8 s.

Espero que te sea de utilidad!