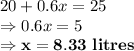Question

From a full 50-liter container of a 40% concentration of acid, x liters are removed and replaced with 100% acid. (A) Write the amount of acid in the final mixture as a function of x (B) Determine the domain and range of the function (C) Determine if the final mixture is 50% acid PLEASE EXPLAIN...I DON'T UNDERSTAND THIS AT ALL

Answer 1

A) 20+0.6
`x`

B) range is [0, 50] (i.e. both inclusive)

C) 8.33 litres

Explanation:

Given that concentration of acid in 50 litre container is 40%.

Amount of acid in the container = 40% of 50 litres

Amount of acid in the container =
`(40)/(100) * 50 = 20\ litre`

`x` litres are removed.

Amount of acid removed = 40% of
`x` litre.

Now, remaining acid in the container = (20 - 40% of
`x`) litre

Now, replaced with 100% acid.

So, final acid in the container = (20 - 40% of
`x` + 100% of
`x` ) litre

Amount of acid in the final mixture:

`20 - (40)/(100) * x + (100)/(100) * x\\\Rightarrow 20 +(100-40)/(100)x\\\Rightarrow 20 +(60)/(100)x`

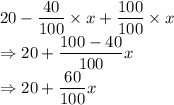
Answer A) Amount of acid in the final mixture = 20+0.6
`x`

Answer B)
`x` can not be greater than 50 litres (initial volume of container) and can not be lesser than 0 litres.

so, range is [0, 50] (i.e. both inclusive)

Answer C)

Given that final mixture is 50% acid.

amount of acid = 50% of 50 litres = 25 litres

Using the equation:

`20+0.6x =25\\\Rightarrow 0.6x =5\\\Rightarrow \bold{x =8.33\ litres}`