Answer:
Number of nickels = 6
Number of dimes = 14
Number of quarters = 23
Explanation:
Total number of coins = 43
Let number of nickels = n
Let number of dimes = d
Let number of quarters = q
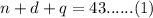
Money in n nickels =
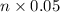
Money in d dimes =
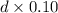
Money in q quarters =
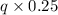
Total money = $7.45
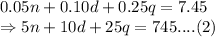
The sum of the numbers of nickels and dimes is 3 less than the number of quarters.
i.e.
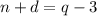
Let us put the value in (1):
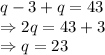
Putting the value of q in (1) and (2):
n+d = 20 .... (3)
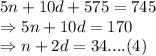
(4) - (3):
d = 14
Now, from (3):
n = 6
Number of nickels = 6
Number of dimes = 14
Number of quarters = 23