Question

Find the point P that partitions the line segment AB given the ratio.

A (3, 6) B(4, 3) with the ratio 2:1

Answer 1

`(11)/(3),4`

Step-by-step explanation:

A line segment XY with points at X(
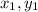`x_1,y_1`) and Y(
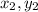`x_2,y_2`) divided by a point O(x, y) in the ratio n:m , the location of point O(x, y) is at:

`x=(n)/(n+m)(x_2-x_1)+x_1\\ \\y=(n)/(n+m)(y_2-y_1)+y_1`

Given line segment AB with location A (3, 6) B(4, 3), point P is given as:

`x=(n)/(n+m)(x_2-x_1)+x_1=(2)/(2+1)(4-3)+3=(2)/(3)(1)+3=(11)/(3) \\ \\y=(n)/(n+m)(y_2-y_1)+y_1=(2)/(2+1)(3-6)+6=(2)/(3)(-3)+6=-2+6=4`

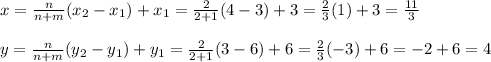
The location of point P is at (
`(11)/(3),4`)