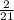Question

If two of these shapes are randomly chosen, one after the other without replacement, what is the probability that both chosen will be triangles?

Answer 1

2/21

Explanation:

There are 4 stars, 5 triangles, 3 circles, and 3 squares

For the first drawing there are 5 triangles and a total of 15 shapes.

p(first triangle) = 5/15 = 1/3

Since there is no replacement, for the second drawing, and one triangle has been taken, now there are 4 triangles left and 14 total shapes left.

p(second triangle) = 4/14 = 2/7

p(two triangles) = p(first triangle) * p(second triangle)

p(two triangles) = 1/3 * 2/7

p(two triangles) = 2/21

Answer 2

`P(T_1\ n\ T_2) = (2)/(21)`

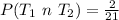
Explanation:

From the comments in your question; we have

Stars = 4

Triangles = 5

Circles = 3

Squares = 3

Required

Determine the probability of both shapes being triangles

First, calculate the total

`Total = 4 + 5 + 3 + 3`

`Total = 15`

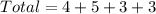
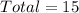
Next, calculate the probability of the first selected shape being a triangle;

P(T₁) = Number of triangles divided by total number of shapes

`P(T_1) = (5)/(15)`

`P(T_1) = (1)/(3)`

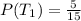
Next, calculate the probability of the second selected shape being a triangle;

P(T₂) = Number of triangles divided by total number of shapes

Because it's probability without replacement. the number of triangle left is 4 and the number of shapes left is 14;

So:

`P(T_2) = (4)/(14)`

`P(T_2) = (2)/(7)`

Hence:

`P(T_1\ n\ T_2) = P(T_1) * P(T_2)`

`P(T_1\ n\ T_2) = (1)/(3) * (2)/(7)`

`P(T_1\ n\ T_2) = (2)/(21)`

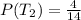
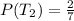
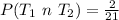
Hence, the required probability is
`(2)/(21)`