Question

Ship A and Ship B are 120 km apart when they pick up a distress call from another boat. Ship B estimates that they are 70 km away from the distress call. They also notice that the angle between the line from ship B to ship A and the line from ship A to the distress call is 28°. What are the two possible distances, to the nearest TENTH of a km, from ship A to the boat?

Answer 1

147.5 km and 64.4 km

Explanation:

a=120 km

b=70 km

β=28 degrees ( ∘)

b^2=(a^2)+(c^2)−2ac*cosβ

70^2 =(120^2 )+(c^2)−2⋅ 120⋅ c⋅ cos(28∘ )

(c^2 ) −211.907c+9500=0

note p, q, and r are replacement variables in the Pythagorean theorem since a, b, and c are already in use

p=1;q=−211.907;r=9500

D=(q^2 ) −4pr=(211.907^2 )−4⋅1⋅9500=6904.75561996

D>0

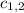`c_(1,2)` = (−q±
`√(D)` )/2p=(211.91±
`√(6904.76)`)/2

​
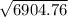`c_(1,2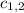)` =105.95371114±41.5474295834

(
`c_(1)`−147.501140726)(
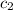`c_(2)`−64.4062815596)=0

`c_(1)`=147.501140726

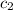`c_(2)`=64.4062815596