Question

Consider the tables that represent a continuous function and its inverse. Which is an accurate comparison of the functions? -9 0 0 27 3 36 12 63 f(x) 9 х – 12 f-1(x) -13 -3 -10 0 -9 6 -7 9 -6 ✓ The reciprocal of the slope of f(x) is the same as the slope of f1(x). The negative reciprocal of the slope of f(x) is the same as the slope of f'(x). The y-coordinate of the y-intercept of f(x) is the same as the y-coordinate of the y-intercept of f'(x). The opposite of the y-coordinate of the y-intercept of f(x) is the same as the x-coordinate of the x-intercept of f'(x). Submitted​

Answer 1

Answer: A

The reciprocal of the slope of f(x) is the same as the slope of f–1(x).

Explanation:

Answer 2

the reciprocal of the slope of f(x) is the same as the slope of f⁻¹(x)

Explanation:

To find the equation of a line given two points, we use the formula:

`y-y_1=(y_2-y_1)/(x_2-x_1) (x-x_1)`

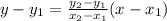
The standard equation of a line is given by:

y = mx + c; where m is the slope of the line and c is the intercept on the y axis

For the function f(x), we have to select two points, let us select (-6, 9) and (0, 27)

Hence the equation of the line f(x) is:

`y-y_1=(y_2-y_1)/(x_2-x_1) (x-x_1)\\\\y-9=(27-9)/(0-(-6))(x-(-6))\\ \\y-9=(18)/(6) (x+6)\\\\y-9=3(x+6)\\\\y-9=3x+18\\\\y=3x+18+9\\\\y=3x+27\\`

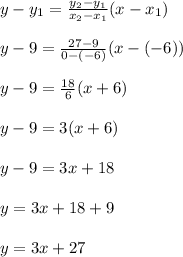
Comparing y = 3x + 27 with y = mx + c, we can see that the slope (m) = 3 and the y intercept is 27

For the inverse function f⁻¹(x), let us use the points (-3, -10) and (0, 9)

Hence the equation of the line f⁻¹((x) is:

`y-y_1=(y_2-y_1)/(x_2-x_1) (x-x_1)\\\\y-(-10)=(-9-(-10))/(0-(-3))(x-(-3))\\ \\y+10=(1)/(3) (x+3)\\\\y+10=(1)/(3)x+1\\\\y=(1)/(3)x+1-10\\\\y=(1)/(3)x-9\\`

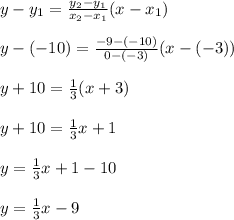
To find the x intercept put y = 0

0 = (1/3)x - 9

(1/3)x = 9

x = 27

Comparing y = (1/3)x - 9 with y = mx + c, we can see that the slope (m) = 1/3 and the y intercept is -9

Hence, the reciprocal of the slope of f(x) is the same as the slope of f⁻¹(x) (i.e reciprocal of 3 = 1/3)