Question

12. The sum of four consecutive numbers in A.P. is 32 and the ratio of the product of the first and last terms to the product of two middle terms is 7:15. Find the number.

Answer 1

2, 6, 10, 14

or

14, 10, 6, 2.

Explanation:

Let the four consecutive numbers in A.P. be a - 3d, a - d, a + d, a + 3d

According to the first condition:

a - 3d + a - d + a + d + a + 3d =32

4a = 32

a = 32/4

a = 8

According to the second condition:

`((a - 3d)(a + 3d))/((a - d)(a + d)) = (7)/(15) \\ \\ \frac{ {a}^(2) - (3d)^(2) }{ {a}^(2) - {d}^(2) } = (7)/(15) \\ \\ \frac{ {a}^(2) - 9d^(2) }{ {a}^(2) - {d}^(2) } = (7)/(15) \\ \\ \frac{ {8}^(2) - 9d^(2) }{ {8}^(2) - {d}^(2) } = (7)/(15) \\ \\ \frac{ 64 - 9d^(2) }{ 64 - {d}^(2) } = (7)/(15) \\ \\ 15(64 - 9 {d}^(2) ) = 7(64 - {d}^(2) ) \\ \\ 960 - 135 {d}^(2) = 448 - 7 {d}^(2) \\ \\ 960 - 448 = 135 {d}^(2) - 7 {d}^(2) \\ \\ 512 = 128 {d}^(2) \\ \\ {d}^(2) = (512)/(128) \\ \\ {d}^(2) = 4 \\ \\ d = \pm 2 \\ \\ when \: d = 2 \\ a - 3d = 8 - 3 * 2 = 8 - 6 = 2 \\ a - d = 8 - 2 = 6 \\ a + d = 8 + 2 = 10 \\ a + 3d = 8 + 3 * 2 = 8 + 6 = 14 \\\\ when \: d = - 2 \\ a - 3d = 8 - 3 * ( -2 ) = 8 + 6 = 14 \\ a - d = 8 -( - 2 )= 8 + 2 = 10 \\ a + d = 8 + ( - 2 )= 8 - 2 = 6\\ a + 3d = 8 + 3 * ( - 2 )= 8 - 6 = 2 \\`

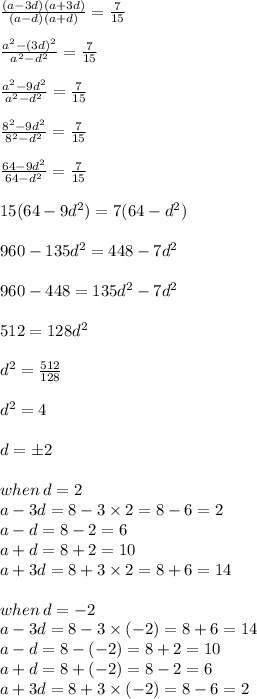
Thus the four consecutive numbers of the A. P. are 2, 6, 10, 14 or 14, 10, 6, 2.