Answer:
(a) 4.83 seconds
(b) 167.3m
(c) 40m
Step-by-step explanation:
This is a two-dimensional motion. Therefore, the components of the initial velocity -
 and
and
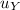 - in the x and y directions are given as follows:
- in the x and y directions are given as follows:
 = u cos θ --------------(*)
= u cos θ --------------(*)
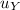 = u sin θ -------------(**)
= u sin θ -------------(**)
Where
θ = angle of projection
(a) To calculate the time taken for the apple to strike the ground.
For simplicity, let's first calculate the maximum height H reached by the apple.
Using one of the equations of motion as follows, we can find H:
v² = u² + 2as ---------------(i)
Where;
v = velocity at maximum height = 0 [at maximum height, velocity is 0]
u = initial vertical velocity of the apple =
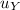
=> u =
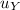 = u sin θ
= u sin θ
=>
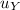 = 40 sin 30°
= 40 sin 30°
=>
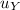 = 40 x 0.5
= 40 x 0.5
=>
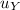 = 20 m/s
= 20 m/s
a = acceleration due to gravity = -g [apple moves upwards against gravity]
a = -10m/s²
s = H = maximum height reached from the top of the building
Substitute these values into equation (i) above to have;
0² =
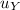 ² + 2aH
² + 2aH
0² = (20)² + 2(-10)H
0 = 400 - 20H
20H = 400
H = 20m
The total time taken to strike the ground is the sum of the time taken to reach maximum height and the time taken to strike the ground from maximum height.
=>Calculate time t₁ to reach maximum height.
Using one of the equations of motion, we can calculate t₁ as follows;
v =
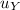 + at ---------------(ii)
+ at ---------------(ii)
Where;
v = velocity at maximum height = 0
u = initial vertical velocity of the apple =
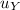
a = -g = -10m/s² [acceleration due to gravity is negative since the apple is thrown upwards to reach maximum height]
t = t₁ = time taken to reach maximum height.
Equation (ii) then becomes;
0 = 20 + (-10)t₁
10t₁ = 20
t₁ = 2 seconds
=>Calculate time t₂ to strike the ground from maximum height.
Now, using one of the equations of motion, we can calculate the time taken as follows;
Δy =
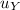 t +
t +
 at ---------------(iii)
at ---------------(iii)
Where;
Δy = displacement from maximum height to the ground = maximum height from top of building + height of building = 20 + 20 = 40m
a = g = 10m/s² [acceleration due to gravity is positive since the apple is now coming downwards from maximum height]
t = t₂ [time taken to strike the ground from maximum height]
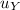 = initial vertical velocity from maximum height = 0
= initial vertical velocity from maximum height = 0
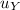 = 0
= 0
Equation (iii) then becomes
40 = 0t +
 (10)t₂²
(10)t₂²
40 = 5t₂² [divide through by 5]
8 = t₂²
t₂ = ±

t₂ = ±
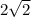
t₂ = +2
 or -2
or -2

since time cannot be negative,
t₂ = 2
 = 2.83 seconds
= 2.83 seconds
Therefore, the time taken for the apple to strike the ground is;
t₁ + t₂ = 2 + 2.83 = 4.83 seconds
(b) The distance from the foot of the building where the apple will strike the ground
Since this is the horizontal distance, we use the horizontal version of equation (iii) as follows;
Δx =
 t +
t +
 at -----------(v)
at -----------(v)
Where
Δx = distance from the foot of the building to where the apple strikes the ground.
 = initial horizontal velocity of the apple as expressed in equation (*)
= initial horizontal velocity of the apple as expressed in equation (*)
 = 40 cos 30
= 40 cos 30
 = 34.64 m/s
= 34.64 m/s
t = time taken for the motion of the apple = 4.83 seconds [calculated above]
a = acceleration due to gravity in the horizontal direction = 0. [For a projectile, there is no acceleration in the horizontal direction since velocity is constant]
Substitute these values into equation (v) as follows;
Δx =
 t +
t +
 (0)t
(0)t
Δx = 34.64 x 4.83
Δx = 167.3 m
Therefore, the distance from the foot of the building is 167.3m
(c) The maximum height reached by the apple from the ground
This is the sum of the height reached from the top of the building (20m which has been calculated in (a) above) and the height of the building.
= 20m + 20m = 40m