Question

The sum of two squares of two consecutive natural numbers is 41.Find the numbers​

Answer 1

★ Solution :

Let the number be x and x + 1.

`\rule{130}1`

`\underline{ \large \purple{ \mathscr{\dag\:A \bf{ccording} \: to \: \mathscr {Q} \bf{uestion} ....}}}`

`:\implies\sf x^2 + (x + 1)^2 = 41 \\\\\\:\implies\sf 2x^2 + 2x + 1 - 41 = 0\\\\\\:\implies\sf 2x^2 + 2x + 40 = 0\\\\\\:\implies\sf x^2 + x - 20 = 0\\\\\\:\implies\sf x^2 + x - 20 = 0\\\\\\:\implies\sf x^2 + x - 20 = 0\\\\\\:\implies\sf x^2 + 5x - 4x - 20 = 0\\\\\\:\implies\sf x(x + 5) - 4(x + 5) = 0\\\\\\:\implies\sf (x + 5)(x - 4) = 0\\\\\\:\implies\underline{\boxed{\sf x = -5, 4}}`

⠀

We know that -5 is not a natural number. Hence, x = 4.

`\therefore\:\underline{\textsf{The two consecutive natural number is \textbf{4 and 5}}}.`

Answer 2

The 2 unknown numbers are 4 and 5 .

Explanation :

Let the numbers be x and x + 1.

From the given information,

`\dashrightarrow\sf \ \ \ x^2 + (x + 1)^2 = 41 \\ \\ \\`

`\dashrightarrow\sf \ \ \ 2 {x}^(2) + 2x + 1 = 41 \\ \\ \\`

`\dashrightarrow\sf \ \ \ 2 {x}^(2) + 2x + 1 - 41=0 \\ \\ \\`

`\dashrightarrow\sf \ \ \ {x}^(2) + x - 20 = 0 \\ \\ \\`

`\dashrightarrow\sf \ \ \ (x + 5)(x - 4)=0 \\ \\ \\`

`\dashrightarrow\sf \ \ \ { \underline{ \boxed{ \bf{ \red{x = - 5,4}}}}} \ \bigstar \\ \\`

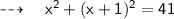
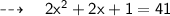
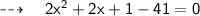
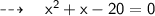
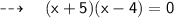
But, as we know -5 is not a natural number,

Hence, x = 4 .

So the 2 unknown numbers are :

• x = 4 [1st number]

• x + 1 = 4 + 1 = 5 [2nd number]

━━━━━━━━━━━━━━━