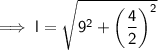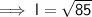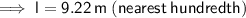Answer:
9.22 m (nearest hundredth)
Explanation:
Volume of a right square pyramid
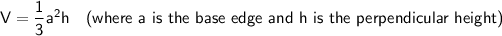
Given:
Substituting the given values into the formula to find h:

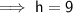
The relationship between the slant height, perpendicular height, and the base edge is given by using Pythagoras' Theorem, where the slant height is the hypotenuse of a right triangle.
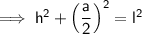
(where l is the slant height, a is the base edge and h is the perpendicular height)
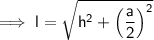
Given:
- h = 9 m (previously calculated)
- a = 4 m
Substituting the given values into the formula to find l: