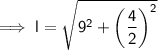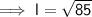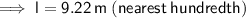Question

DESPERATE HELP NEEDED!! WITH EXPLANATION PLEASE. 60 POINTSSSSS

The volume of the following square pyramid is 48m^3 and has a base edge of 4. What is the length of 'l' the slant height? Round your answer to the nearest hundredth.

Answer 1

9.22 meters

Explanation:

The formula for a pyramid is (base * height) / 3. Therefore, because it's a square, the base is 16, and thus the height divided by 3 = 3. 3 * 3 = 9, so the height is 9. Now we have a right triangle.

If the base edge = 4, half of the base edge is 2. Applying the Pythagorean Theorem, 2^2 + 9^2 = x^2 so then 4 + 81 = x^2. The square root of 85 is approximately 9.22 meters.

Answer 2

9.22 m (nearest hundredth)

Explanation:

Volume of a right square pyramid

`\sf V=(1)/(3)a^2h\quad \textsf{(where a is the base edge and h is the perpendicular height)}`

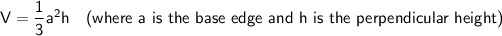
Given:

• V = 48 m³
• a = 4 m

Substituting the given values into the formula to find h:

`\sf \implies 48=(1)/(3)(4)^2h`

`\implies \sf h=9`

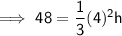
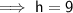
The relationship between the slant height, perpendicular height, and the base edge is given by using Pythagoras' Theorem, where the slant height is the hypotenuse of a right triangle.

`\implies \sf h^2+\left((a)/(2)\right)^2=l^2`

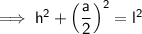
(where l is the slant height, a is the base edge and h is the perpendicular height)

`\sf \implies l=\sqrt{h^2+\left((a)/(2)\right)^2}`

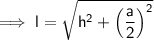
Given:

• h = 9 m (previously calculated)
• a = 4 m

Substituting the given values into the formula to find l:

`\sf \implies l=\sqrt{9^2+\left((4)/(2)\right)^2}`

`\sf \implies l=√(85)`

`\sf \implies l=9.22\:m\:(nearest\:hundredth)`