Question

Can someone answer this circle equation question? PLEASE SHOW STEPS

Answer 1

A

Explanation:

oh steps are here!

Answer 2

a) 5

Explanation:

2x² - 6x + 2y² + 2y = 45

Complete the square and get it in the form (x-a)² + (y -b)² = r²

2x² - 6x + 2y² + 2y = 45

Divide the equation by 2

x² - 3x + y² + y = 45/2

x² - 3x + ? + y² + y + ?? = 45/2

? -----> (x coefficient by 2)² = (3/2)² = 9/4

?? ----> (y coefficient by 2)² = (1/2)² = 1/4

Add (9/4) & (1/4) to both sides,

x² -3x +(9/4) + y² + y + (1/4) = (45/2)+ (9/4) + (1/4)

(x - 3/2)² + (y + 1/2)² = (90/4) + (9/4) + (1/4)

`(x-(3)/(2))^(2)+(y+(1)/(2))^(2)=(90+9+1)/(4)\\\\\\(x-(3)/(2))^(2)+(y+(1)/(2))^(2)=(100)/(4)\\\\\\(x-(3)/(2))^(2)+(y+(1)/(2))^(2)=25\\\\(x-(3)/(2))^(2)+(y+(1)/(2))^(2)=5^(2)`

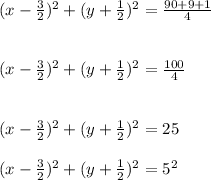
Radius = 5