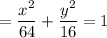Question

Write the equation in standard form for the ellipse with center at the origin, vertex (-8, 0), and co-vertex (0,4).​

Answer 1

Answer:
`(x^2)/(64)+(y^2)/(16)=1`

Explanation:

The standard form for an ellipse is:
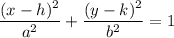`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1` where

• (h, k) is the center
• a is the radius on the x-axis
• b is the radius on the y-axis

Given: (h, k) = (0, 0)

a = 8 (distance on x-axis from origin to -8)

b = 4 (distance on y-axis from origin to 4)

Input h = 0, k = 0, a = 8, b = 4 into the standard form for an ellipse:

`((x-0)^2)/(8^2)+((y-0)^2)/(4^2)=1`

`=(x^2)/(64)+(y^2)/(16)=1`