Answer:
The pulling force F is 200 N
Step-by-step explanation:
We note that the tension in a rope between two or three blocks is given by the relation;
Where we have;
m₁ → T₁ → m₂ → T₂ → m₃ → F
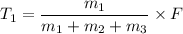
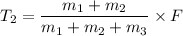
m₁ = 2 kg
m₂ = 4 kg
m₃ = 4 kg
T₂ = 120 N
Therefore, by substitution, gives;
2 kg → T₁ → 4 kg → 120 N → 4 kg → F
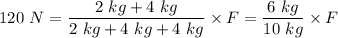
F = 120 N × (10 kg)/(6 kg) = 200 N
The pulling force F = 200 N.