Question

The product of two whole numbers is 936 and the sum is 62. What are the two numbers

Answer 1

26 and 36.

Explanation:

Let the two whole numbers be a and b. Thus, the product of them is 936 while their sum is 62. In equations, this is:

`ab=936\\a+b=62`

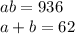
This is a system of equations. To solve, subtract either a or b from the second equation and substitute it into the first.

For instance, subtract b from both sides in the second equation:

`a+b=62\\a=62-b`

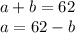
Substitute this into the first equation:

`(62-b)(b)=936`

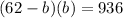
Distribute:

`62b-b^2=936`

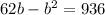
Rearrange:

`-b^2+62b=936`

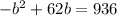
Divide everything by -1 to make the leading coefficient positive:

`b^2-62b=-936`

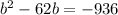
Add 936 to both sides:

`b^2-62b+936=0`

This is now a quadratic. Solve for b.

To do so, we can factor.

After a bit of testing, we can see that -36 and -26 are possible. Thus:

`(b-26)(b-36)=0`

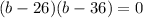
For for b:

`b=26\text{ or } b=36`

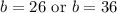
Thus, b is 26 or 36.

Now, plug these back into the isolated equation to solve for a:

`a=62-b\\a=62-(26) \text{ or } a=62-(36)\\a=36\text{ or } a=26`

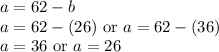
It doesn't really matter which one we choose since they're the same.

Thus, the answer is 26 and 36.