Question

Two positively charged particles are first brought close together and then released. Once released, the repulsion between particles causes them to move away from each other. (a) This is an example of potential energy being converted into what form of energy? (b) Does the potential energy of the two particles prior to release increase or decrease as the distance between them is increased.

Answer 1

(a) Kinetic energy.

(b) The potential energy between the two particles will decrease as they move away from each other.

Step-by-step explanation:

(a)

The question seems to imply that the two particles were not moving before they were released. In that case, both particles will have a kinetic energy of zero.

However, once the two particles are released and start to move away from each other, their speed increases. That corresponds to an increase in their kinetic energies. As these particles move away from each other, their kinetic energy continues to increase. Note that electrical repulsion is the force that accelerated the two particles. Therefore, conclude that the (electrical) potential energy of the two particles is converted to kinetic energy.

(b)

Let
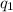`q_1` and
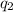`q_2` denote the charge on the two particles. Let
`r` denote the distance between them. Assume that the sizes of these two particles are much smaller than the distance between them. Let
`k` represent the Coulomb Constant. The size of the electrical potential energy between the two particles would be:

`\displaystyle E = (k\, q_1\, q_2)/(r)`,

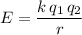Based on these assumptions, the size of the electrical potential energy between the two particles is inversely proportional to the distance between them. Increasing the distance between the two particles would reduce the size of the electrical potential energy.