Question

Answer the question quick​

Answer 1

x²+6x-15

Explanation:

We are given this expression:

`(3x^2+2x-8) - ( 2x^2-4x+7)`

We want to simplify the expression. First, distribute the negative sign in front of the second set of parentheses. Multiply each term inside the parentheses by -1.

`(3x^2+2x-8) + (-1*2x^2) + (-1*-4x) + (-1*7)`

`(3x^2+2x-8) -2x^2+ 4x -7`

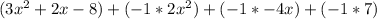
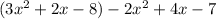
Next, combine like terms. The 2 terms with an x² can be combined, just like the two terms with an x, and the two terms without a variable.

`(3x^2-2x^2) + (2x+4x) + (-8-7)`

`x^2+(2x+4x)+(-8-7)`

`x^2+6x+(-8-7)`

`x^2+6x-15`

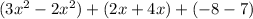
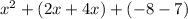
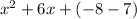
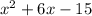
The expression x²+6x-15 is equivalent to (3x²+2x-8)-(2x²-4x+7)

Answer 2

x^2 +6x -15

Explanation:

(3x^2 +2x -8) - (2x^2 -4x+7)

Distribute the minus sign

(3x^2 +2x -8) - 2x^2 +4x-7

Combine like terms

x^2 +6x -15