Question

A test consists of 20questions. Multiple choice questions earn 4points for a correct answer, and free response questions earn 8points for a correct answer. If the test is out of 100points, how many of each type of question are on the test?

Answer 1

15 multiple choice questions

5 free response questions

Explanation:

This is basically a systems of equations word problem.

To solve this, we need to create two equations that represent this scenario. Let's suppose
`m` represents the amount of multiple choice questions and
`f` represents the amount of free-choice questions.

We can create the following equations:

`4m + 8f = 100`

`m+f=20`

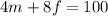
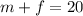
To solve for m and f, we can use elimination.

Let's multiply the equation
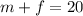`m+f=20` by -4.

`-4m - 4f = -80`

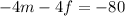
Great! Now let's add this equation to our first one,
`4m + 8f = 100`.

`4m + 8f = 100`

`-4m - 4f = -80`

___________________

`0m + 4f = 20`

`4f=20`

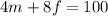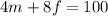
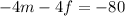
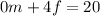
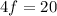
Dividing both sides by 4 get us
`f=5`.

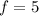So there are 5 free choice questions. To find m, we can substitute inside the equation
`m+f=20`

`m+5=20\\\\m=20-5\\\\m=15`

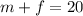
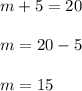
So there are 15 multiple choice questions.

Hope this helped!