Question

HELP!!!!!!!!!! AP CALCULUS AB

Answer 1

`\lim_(x \to 5^-)f(x)=54\\\lim_(x \to 5^+)f(x)=-17`

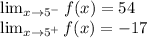
Explanation:

So, we have the function:

`f(x)=x^2+5x+4,x<5\\f(x)=8,x=5\\f(x)=-4x+3,\text{ otherwise}`

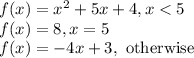
And we want to show that this has a jump discontinuity.

As directed, calculate the limit at x=5 from the left and from the right. Thus:

`\lim_(x \to 5^-)f(x)`

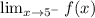
To calculate this, since we're coming from the left, x is less than 5. So, use the first equation:

`\lim_(x \to 5^-)f(x)\\= \lim_(x \to 5^-)(x^2+5x+4)\\`

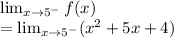
Use direct substitution:

`=(5)^2+5(5)+4\\=25+25+4\\=54`

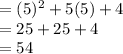
Thus, as the limit approaches f(5) from the left, the function approaches 54.

Now, calculate the limit at x=5 from the right. Since we're coming from the right, use the third equation:

`\lim_(x \to 5^+)f(x)\\= \lim_(x \to 5^+)(-4x+3)`

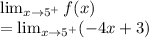
Direct substitution:

`(-4(5)+3)\\=-20+3\\=-17`

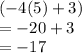
Thus, as the limit approaches f(5) from the right, the function approaches -17.

As you can picture, there's a huge gap between y=54 and y=-17. The limits are not equal and both of the limits do exist. Thus, we have jump discontinuity.

Answer 2

`\lim_(x \to 5^(-)) f(x)= 54`

`\lim_(x \to 5^(+)) f(x) = -17`

Explanation:

+ means we are approaching from the right

- means we are approaching from the left

We are given that if x < 5, it is x² + 5x + 4

So to find
`\lim_(x \to 5^(-)) f(x)` we would plug in 5 into that piecewise function part:

5² + 5(5) + 4 = 54

We would be approaching y = 54 if we approach from the left.

We are given that x > 5, it is -4x + 3

So to find
`\lim_(x \to 5^(+)) f(x)` we would plug in 5 into that piecewise function part:

-4(5) + 3 = -17

We would approach y = -17 if we approached from the right.