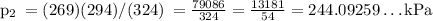Question

If anyone is good at chemistry do you mind helping :)

Answer 1

• 1.62432 moles of nitrogen

• Tire Pressure: 2.74 * 10⁵ Pa

• The tires will burst

• Pressure: 244 kPa

Step-by-step explanation:

• We can determine the number of moles of nitrogen using the formula pV = nRT, where p = pressure, V = volume, n = number of moles, R = gas constant, and T = absolute temperature.

Now remember we have our initial pressure in kilopascals so let's convert to pascals (249 pascals). The volume is given in liters, so let's convert into m². And the initial temperature is given in Celsius ⇒ our absolute temperature in Kelvins.

`\mathrm{p\:}=\mathrm{249 kPa\:} = \mathrm{2.49 * 10^5\:},\\\mathrm{15.6L\:} =\mathrm{0.0156m^2\:},\\\mathrm{R\:}=\mathrm{8.314J/mol*K\:},\\\mathrm{T\:}=\mathrm{21C\:} + \mathrm{273\:}=\mathrm{294K\:}`

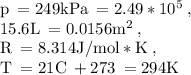
Respectively the moles of nitrogen in each tire should be:

`\mathrm{n\:}=\mathrm{pV/RT\:}=\mathrm{(2.49*10^5)(0.0156)/(8.314)(294)\:}=(\left(2.49\cdot \:10^5\right)\left(0.0156\right))/(\left(8.134\right)\left(294\right))=(3884.4)/(2391.396)\\`

`= 1.62432\dots \mathrm{moles\:}\mathrm{of\:}\mathrm{nitrogen\:}`

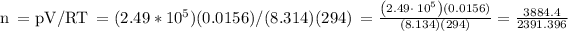
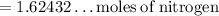
• We can solve this part similarly. All our values will be the same, besides the temperature, as we have to consider both the initial and final temperature here.

`\mathrm{T_2\:}=\mathrm{51C+ 273\:} }=\mathrm{324K\:} }` -

`\mathrm{p_2\:}=\mathrm{(2.49*10^5)(324)/(294)\:} }=(\left(2.49\cdot \:10^5\right)\left(324\right))/(294)=(40338000)/(147)=274408.16326\dots`

`=2.74408.16326*10^5\dots\mathrm{Pa}`

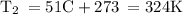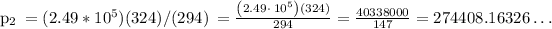
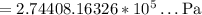
• The text mentions that the tires will burst when the internal pressure reaches 269kP. From part #2 we know that the final pressure will be, in kilopascals, 274kP. As 274 > 269, the tires will burst in Death Valley.

• We would want the final temperature = breaking pressure. Therefore,

`\mathrm{p_2\:}=\mathrm{(269)(294)/(324)\:} }=(79086)/(324)=(13181)/(54)=244.09259\dots\mathrm{kPa\:} }`