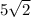Answer:
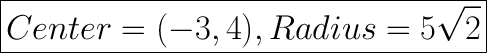
Explanation:
Given equation is
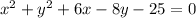
Adding 25 to both sides
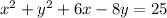
Completing squares
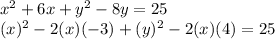
Both of their "b" is -3 and 4 respectively
So, adding (-3)² => 9 and (4)² => 16 to both sides
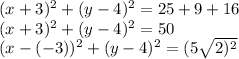
Comparing it with
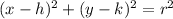 , where center = (h,k) and radius = r.
, where center = (h,k) and radius = r.
We get:
Center = (-3,4)
Radius =