Question

Please explain How you got the Answer

Answer 1

The radius is
`2√(15)`

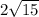
The center is (3, 3)

Explanation:

Equation of circle in standard form with center at (h, k) and radius r:

`(x - h)^2 + (y - k)^2 = r^2`

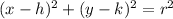
We need to complete the square in x and y.

`x^2 + y^2 - 6x - 6y = 42`

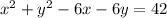
Separate x-terms and y-terms:

`x^2 - 6x + ~~~~~y^2 - 6y + ~~~~~ = 42 + ~~~~~ + ~~~~~`

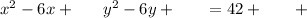
To complete the square, you square half of the linear term's coefficient.

Linear term in x: -6x

Coefficient: -6

Half of the coefficient: -3

Square half of the coefficient: 9

We need to add 9 to both sides to complete the square in x.

The linear term in y is -6y, so we do the same and we also need to add 9 to both sides to complete the square in y.

`x^2 - 6x + 9 + y^2 - 6y + 9 = 42 + 9 + 9`

`(x - 3)^2 + (y - 3)^2 = 60`

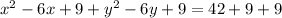
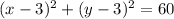
Now that we have the equation in standard form, we can get the radius and center of the circle.

`r^2 = 60`

`r = √(60)`

`r = √(4 * 15)`

`r = 2√(15)`

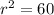
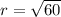
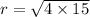
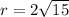
The radius is
`2√(15)`

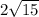
The center is (3, 3)