Question

How can I solve question b). ?

Answer 1

It was not my intention to post that answer, as it does not solve the question, but hope it helps somehow.

Explanation:

`$\text{b)} (\sin(a))/(\sin(a)-\cos(a)) - (\cos(a))/(\cos(a)-\sin(a)) = (1+\cot^2 (a))/(1-\cot^2 (a)) $`

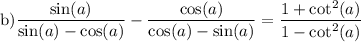
You want to verify this identity.

`$(\sin(a)(\cos(a)-\sin(a)))/((\sin(a)-\cos(a))(\cos(a)-\sin(a))) - (\cos(a)(\sin(a)-\cos(a)))/((\sin(a)-\cos(a))(\cos(a)-\sin(a))) = (1+\cot^2 (a))/(1-\cot^2 (a)) $`

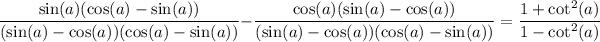
The common denominator is

`(\sin(a)-\cos(a))(\cos(a)-\sin(a))= \boxed{2\cos (a)\sin(a)-\cos ^2(a)-\sin ^2(a)}`

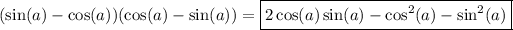
Solving the first and second numerator:

`\sin(a)(\cos(a)-\sin(a))=\sin(a)\cos(a)-\sin^2(a)`

`\cos(a)(\sin(a)-\cos(a))= \cos(a)\sin(a)-\cos^2(a)`

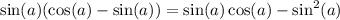
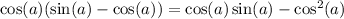
Now we have

`$( \sin(a)\cos(a)-\sin^2(a) -(\cos(a)\sin(a)-\cos^2(a)))/(2\cos (a)\sin(a)-\cos ^2(a)-\sin ^2(a))$`

`$( -\sin^2(a) +\cos^2(a))/(2\cos (a)\sin(a)-\cos ^2(a)-\sin ^2(a))$`

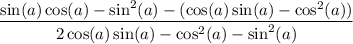
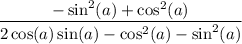
Once

`-\sin^2(a) +\cos^2(a) = \cos(2a)`

`2\cos (a)\sin(a) = \sin(2a)`

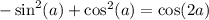
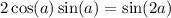
Also, consider the identity:

`\boxed{\sin^2(a)+\cos^2(a)=1}`

`$( -\sin^2(a) +\cos^2(a))/(2\cos (a)\sin(a)-\cos ^2(a)-\sin ^2(a))=\boxed{( \cos(2a))/(\sin(2a)-1)}$`

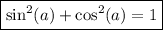
That last claim is true.