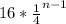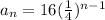Answer:
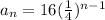
Explanation:
Given:
Fifth term of a geometric sequence =
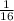
Common ratio (r) = ¼
Required:
Formula for the nth term of the geometric sequence
Solution:
Step 1: find the first term of the sequence
Formula for nth term of a geometric sequence =
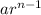 , where:
, where:
a = first term
r = common ratio = ¼
Thus, we are given the 5th term to be ¹/16, so n here = 5.
Input all these values into the formula to find a, the first term.
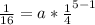
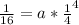
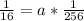

Cross multiply
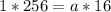
Divide both sides by 16
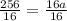

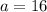
Step 2: input the value of a and r to find the nth term formula of the sequence
nth term =
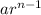
nth term =