Answer:
Choice C.
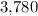 .
.
Explanation:
The word "
 " contains nine letters:
" contains nine letters:
- Four
 's,
's, - Two
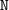 's,
's, - Two
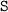 's, and
's, and - One
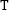 .
.
If all these nine letters are unique, the number of possible arrangements would be:
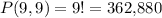 .
.
However, because some of these letters were not unique, a large number of that
 arrangements would be duplicates. What would be the exact number of duplicates? Start by considering giving each of the duplicate letters an index number. For example, consider the duplicates due to the letter "
arrangements would be duplicates. What would be the exact number of duplicates? Start by considering giving each of the duplicate letters an index number. For example, consider the duplicates due to the letter "
 ". There are four
". There are four
 's in
's in
 . Label them as
. Label them as
 ,
,
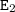 ,
,
 , and
, and
 :
:
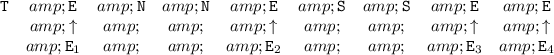 .
.
These four
 can be shuffled and rearranged to give a large number of duplicates:
can be shuffled and rearranged to give a large number of duplicates:
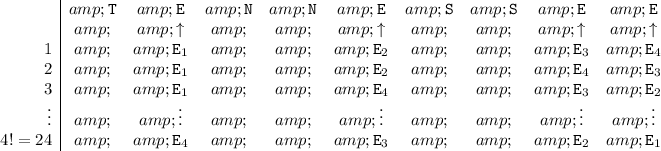 .
.
Each of these duplicate corresponds to a unique way for arranging four unique item in a row. There are
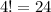 ways to arrange four unique items in a row. Therefore, for each arrangement that is truly unique, the letter "
ways to arrange four unique items in a row. Therefore, for each arrangement that is truly unique, the letter "
 " alone would have caused the arrangement to be counted
" alone would have caused the arrangement to be counted
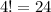 times if the nine letters were assumed to be unique.
times if the nine letters were assumed to be unique.
At the same time, letters "
 " and "
" and "
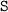 " would further exaggerate the count by a factor of
" would further exaggerate the count by a factor of
 each. On the other hand, the letter
each. On the other hand, the letter
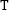 appeared only once and would not create duplicates.
appeared only once and would not create duplicates.
Overall, if the nine letters were assumed to be unique, each arrangement that is truly unique would have been counted:
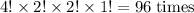 .
.
The count based on the incorrect assumption (that the nine letters are all distinct) is
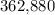 . Divide that count by the factor of exaggeration (
. Divide that count by the factor of exaggeration (
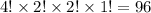 ) to find the number of arrangements that are truly unique:
) to find the number of arrangements that are truly unique:
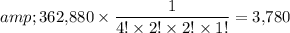 .
.