Answer:
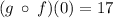
Explanation:
f(x) = 2x + 4
g(x) = 4x² + 1
In order to find (g ∘ f)(0) we must first find
(g ° f )(x)
To find (g ° f )(x) substitute f(x) into g(x) that's for every x in g(x) replace it with f(x)
That's

We have
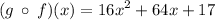
Now to find (g ∘ f)(0) substitute the value of x that's 0 into (g ∘ f)(0)
We have
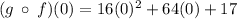
We have the final answer as
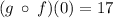
Hope this helps you