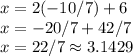Answer:
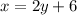
Explanation:
So we have the system:
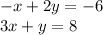
If we isolate the x-variable in the first equation:
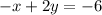
Subtract 2y from both sides:
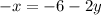
Divide both sides by -1:
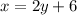
Therefore, we would substitute the above into the second equation:
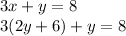
The answer is 2y+6
Further notes:
To solve for the system, distribute:
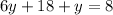
Simplify:
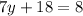
Subtract:
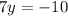
Divide:
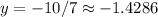
Now, substitute this value back into the isolated equation: