Answer:
(See explanation below for further details)
Explanation:
A. What details can you determine about the dive from the coordinates of the point (5, -8)?
First component corresponds to time and second component to depth with respect to sea level. The diver is 8 feet below sea level at 5 seconds.
B. What is the average speed of the diver in the water? How can you tell from the graph?
The average speed of the diver (
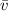 ), measured in feet per second, can be calculated by the following expression:
), measured in feet per second, can be calculated by the following expression:
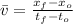
Where:
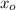 ,
,
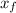 - Initial and final depth of diver, measured in feet.
- Initial and final depth of diver, measured in feet.
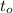 ,
,
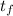 - Initial and final instant, measured in seconds.
- Initial and final instant, measured in seconds.
There are three different average speeds: (i) Descent (
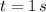 to
to
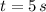 ), (ii) Ascent (
), (ii) Ascent (
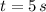 to
to
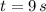 ), (iii) Descent + Ascent (
), (iii) Descent + Ascent (
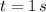 to
to
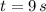 )
)
(i) Descent (
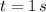 to
to
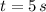 )
)
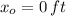 and
and
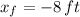
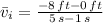
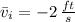
(ii) Ascent (
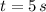 to
to
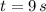 )
)
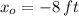 and
and
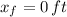
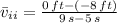
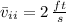
(iii) Descent + Ascent (
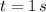 to
to
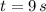 )
)
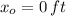 and
and
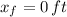
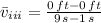
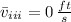
C. Which point on the graph shows the starting location of the diver?
The initial location is when
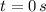 , which corresponds to the intercept of the line on y-axis.
, which corresponds to the intercept of the line on y-axis.