Question

Write an equation parallel to the line determined by the points (15, -6) and (-3, 13), through: (4, 2)

Answer 1

Answer:y=-1.583x-8.332

Explanation:

First find slope from two points (-6-13)/(15+3)=-1.583

Now line is parallel so the slope would be same for the other line passing through (4,2) now as the general equation of line is

y=mx+c

2=-1.583(4)+c

Solving for c equals to -8.332

So final equation is

y=1.583x-8.332

Answer 2

The answer is

`y = - (19)/(18) x + (76)/(2)`

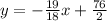
Explanation:

Equation of a line is y = mx + c

where

m is the slope

c is the y intercept

To find the equation of the parallel line we must first find the slope of the original line

That's

Slope of the through points

(15, -6) and (-3, 13) is

`m = (13 - - 6)/( - 3 - 15) = - (19)/(18)`

Since the lines are parallel their slope are also the same

So slope of parallel line = - 19/18

Equation of the line using point (4,2) and slope -19/18 is

`y - 2 = - (19)/(18) (x - 4) \\ y - 2 = - (19)/(18) x + (38)/(9) \\ y = - (19)/(18) x + (38)/(9) + 2`

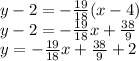
We have the final answer as

`y = - (19)/(18) x + (76)/(2)`

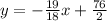
Hope this helps you