Find the radius and the center of the circle with the given equation x2+y2−6x−8y−30=0.

Question

asked May 20, 2021 134k views

2 Answers

Xline · Answer 1 · 2021-05-23T21:33:11+0000

Answer:

Center is (3,4)

Radius is √55 which is approximately 7.42

Explanation:

First, recall the equation for a circle. The equation for a circle is given by:

(x-h)^2+(y-k)^2=r^2

Where (h,k) is the center and r is the radius.

We have the equation:

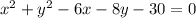
x^2+y^2-6x-8y-30=0

Thus, we want to turn this into the circle equation.

To do so, we need to complete the square.

First, put all the x-terms together and all the y-terms together. Also, add 30 to both sides:

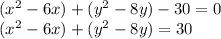
$(x^2-6x)+(y^2-8y)-30=0\\(x^2-6x)+(y^2-8y)=30$

Now, complete the square for both of the variables. Recall how to complete the square. If we have:

x^2+bx

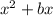
We divide b by 2 and then square it. Then we will have a perfect square trinomial. To keep things balanced, we must also subtract what we added.

Thus, for the first term:

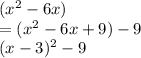
$(x^2-6x)\\=(x^2-6x+9)-9\\(x-3)^2-9$

And for the second term:

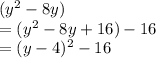
$(y^2-8y)\\=(y^2-8y+16)-16\\=(y-4)^2-16$

Replace the two terms:

((x-3)^2-9)+((y-4)^2-16)=30

Simplify. Add -9 and -16:

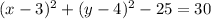
(x-3)^2+(y-4)^2-25=30

Add 25 to both sides:

(x-3)^2+(y-4)^2=55

This is now in the form of the circle equation.

Thus, the center is (3,4).

And the radius is √55 which is approximately 7.42