Newton's Law of Cooling:
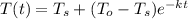
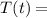 Temperature given at a time
Temperature given at a time
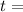 Time
Time
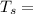 Surrounding temperature
Surrounding temperature
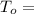 Initial temperature
Initial temperature
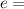 Constant (Euler's number) ≈ 2.72
Constant (Euler's number) ≈ 2.72
 Constant
Constant
Using this information, find the value of
 , to the nearest thousandth, then use the resulting equation to determine the temperature of the water cup after 4 minutes.
, to the nearest thousandth, then use the resulting equation to determine the temperature of the water cup after 4 minutes.
First, plug in the given values in the equation and solve for
 :
:
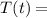 197°,
197°,
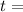 1.5 minutes,
1.5 minutes,
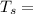 70° and
70° and
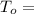 210°
210°
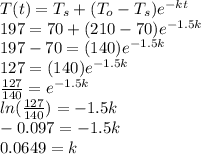
 ≈
≈

Let the temperature of the water cup after
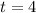 minutes be
minutes be
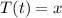
Now, let's plug the new time and
 constant in the equation and solve for
constant in the equation and solve for
 :
:
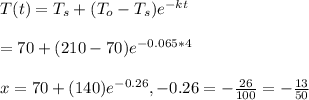
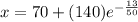
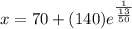

![x=70+{\frac{140}{\sqrt[50]{e^(13)}}\\](https://img.qammunity.org/2021/formulas/mathematics/high-school/e3ot4bi2b162ni6sovy81vzk5j9yx1n0ak.png)
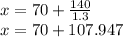
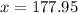 ≈
≈

Temperature of water after 4 minutes is 178°
sorry if there's any misspelling or wrong step but I hope my answer is correct ':3