Question

Please Help! I'm Stuck!

Answer 1

19

Explanation:

Assuming that
`l` represents length and
`w` represents width, we can make a systems of equations and solve for l and w.

`2l+2w=60`, since the perimeter of a rectangle will be double the length plus double the width.

Also we can make the equation
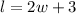`l = 2w+3`, as stated in the last part of the question.

We can now substitute the value of
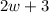`2w+3` into the equation
`2l+2w=60` as l.

`2(2w-3) + 2w = 60\\\\4w-6+2w=60\\\\6w-6=60\\\\6w=66\\\\w = 66/6\\\\w = 11`

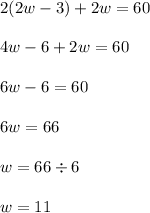
So we know the width is 11. Now that we know the width, we can substitute it back into the equation
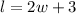`l = 2w+3` to find the length.

`l=2\cdot11-3\\\\l=22-3\\\\l=19`

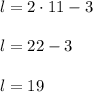
So the length is 19.

Hope this helped!