Answer:
1.
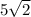
2.
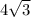
3.

Explanation:
Number 1:
We can treat
 as a variable in which we are multiplying 4 by. Let's call
as a variable in which we are multiplying 4 by. Let's call
 x.
x.
This makes our expression
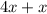 . Combining like terms, we get
. Combining like terms, we get
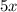 . This means that
. This means that
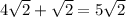 .
.
Number 2:
Again, we can use the same logic as we did in number 1. Let's treat
 as a variable y.
as a variable y.

Subtracting a y term from a y term will equal the difference between the coefficients times y. So it's
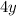 . This means that
. This means that

Number 3:
When we multiply radicals, we want to put the radicals in
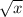 form.
form.
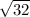 is already in this form.
is already in this form.
However
 is not.
is not.
 is the same thing as
is the same thing as
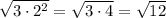 .
.
Now we multiply these radicals by multiply the term inside the square root sign
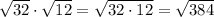
384 is divisible by 64, so:
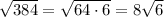
Hope this helped!