Answer:
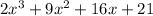
Explanation:
So we have the expression:
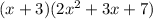
Use the distribute property. Multiply each term on the right by (x+3):
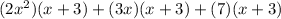
Distribute further:
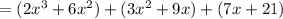
Combine like terms:
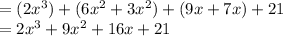
A polynomial in standard form has terms in descending order based on degree.
And we have that. Thus, we are done :)