Question

I) 43x + 31y = 98
31x + 43y = 50

Answer 1

The solution to the system of linear equations
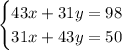`\( \begin{cases} 43x + 31y = 98 \\ 31x + 43y = 50 \end{cases} \)` is
`\( x = (1332)/(449) \) and \( y = (160)/(27) \).`

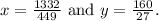
Step-by-step explanation:

To solve the system of equations, we can use the elimination method. Start by multiplying the first equation by 43 and the second equation by 31 to make the coefficients of 'y' the same:

`\[ \begin{cases} 1859x + 1333y = 4214 \\ 961x + 1333y = 1550 \end{cases} \]`

Now, subtract the second equation from the first to eliminate 'y':

`\[ (1859x + 1333y) - (961x + 1333y) = 4214 - 1550 \]`

This simplifies to:

`\[ 898x = 2664 \]`

Divide both sides by 898 to find 'x':

`\[ x = (2664)/(898) = (1332)/(449) \]`

Now, substitute the value of 'x' into one of the original equations; let's use the first one:

`\[ 43\left((1332)/(449)\right) + 31y = 98 \]`

Simplify and solve for 'y':

`\[ 31y = 98 - (57036)/(449) \]`

`\[ 31y = (3906)/(449) \]`

`\[ y = (160)/(27) \]`

Therefore, the solution to the system of equations is
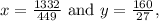`\( x = (1332)/(449) \) and \( y = (160)/(27) \),` representing the point where the two lines intersect.

Answer 2

There are no solutions to the given system of equations.

Hope this helps.