Question

Sum of the numerator and denominator of the fraction is 4 more than twice the numerator . If the numerator and denominator is deceased by 3.they are in the ratio 2:3. Determine the fraction

Answer 1

The system is:

`(x)/(y)=2x + 4`

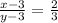`(x-3)/(y-3)=(2)/(3)` (y musn't be 3).

Solving for y in the first equation gives you:

`y=(x)/(2x+4)`

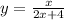
Simplify the second equation to:

`2(y-3)=3(x-3)`

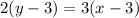
Insert y you solved in first equation to second equation to get:

`(x)/(x+2)-6=3x-3`

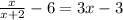
Further simplification gets you to quadratic equation:

`x=(3x+3)(x+2)\implies x=3x^2+9x+6`
`3x^2+8x+6=0`.

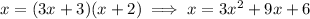
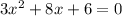Solving quadratic equation using quadratic formula gives you two solutions of x in complex plane:

`x_1=\boxed{-(8)/(6)+(√(8))/(6)i}`

`x_2=\boxed{-(8)/(6)-(√(8))/(6)i}`

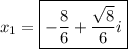
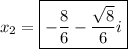
Insert the found x-es into first equation to find the y-s:

`y_1=\boxed{-(1)/(2)+(√(2))/(2)i}`

`y_2=\boxed{-(1)/(2)-(√(2))/(2)i}`

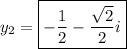
So there are two solutions (points)
`P_1(x_1,y_1),P_2(x_2,y_2)` both in
`\mathbb{C}` plane.

And the two fractions are:

`(-(8)/(6)+(√(8))/(6)i)/(-(1)/(2)+(√(2))/(2)i)`.

`(-(8)/(6)-(√(8))/(6)i)/(-(1)/(2)-(√(2))/(2)i)`.

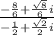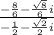Hope this helps.