Question

B) The price of an electric fan is fixed 20% above its cost price. When it is sold allowing

18% discount, there is a loss of Rs 20. Calculate the marked price and the selling price
of the fan.
​

Answer 1

`\boxed{ \boxed{ \sf {Marked \: price \: = Rs \: 1500}}}`

`\boxed{ \bold{ \boxed{ \sf{Selling \: price = \: Rs \: 1230}}}}`

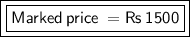
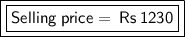
Explanation:

Let Cost price ( C.P ) be x

Finding the Marked price and selling price

Marked price =
`\sf{x + 20\% \: of \: x}`

⇒
`\sf{x + (20)/(100) * x}`

⇒
`\sf{ (x * 100 + 20x)/(100) }`

⇒
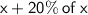
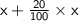
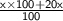
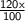`\sf{ (120x)/(100) }` ⇒ ( i )

Selling price =
`\sf{marked \: price \: - 18\% \: of \: marked \: price}`

⇒
`\sf{ (120x)/(100) - (18)/(100) * (120x)/(100) }`

⇒
`\sf{ (120x)/(100) - (54x)/(250) }`

⇒
`\sf{ (120x * 5 - 54x * 2)/(500) }`

⇒
`\sf{ (600x - 108x)/(500) }`

⇒
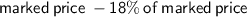
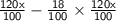
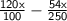
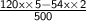
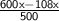
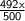`\sf{ (492x)/(500) }` ⇒ ( ii )

Finding the value of x ( Cost price )

`\sf{loss = cost \: price - selling \: price}`

⇒
`\sf{20 = x - (492x)/(500) }`

⇒
`\sf{20 = (x * 500 - 492x)/(500) }`

⇒
`\sf{20 = (8x)/(500) }`

⇒
`\sf{8x = 10000}`

⇒
`\sf{x = (10000)/(8) }`

⇒
`\sf{x = \: Rs \: 1250}`

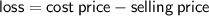
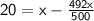
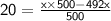
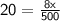
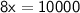
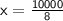
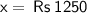
Value of x ( cost price ) = Rs 1250

Now, Replacing the value of x in ( i ) in order to find the value of marked price

`\sf{marked \: price = (120x)/(100) }`

⇒
`\sf{ (120 * 1250)/(100) }`

⇒
`\sf{ \: Rs \: 1500}`

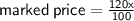
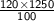
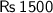
Replacing value of x in ( ii ) in order to find the value of selling price

`\sf{selling \: price = (492 \: x)/(500) }`

⇒
`\sf{ (615000)/(500) }`

⇒
`\sf{ \: Rs \: 1230}`

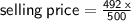
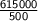
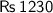
Thus , Marked price of the fan = Rs 1500

Selling price of the fan = Rs 1230

Hope I helped!

Best regards!!