Question

a ball of mass 100g moving at a velocity of 100m/s collides with another ball of mass 400g moving at 50m/s in same direction, if they stick together calculate the velocity and loss of energy​

Answer 1

Velocity of the two balls after collision:
`60\; \rm m \cdot s^(-1)`.

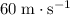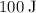`100\; \rm J` of kinetic energy would be lost.

Step-by-step explanation:

Velocity

Because the question asked about energy, convert all units to standard units to keep the calculation simple:

• Mass of the first ball:
  `100\; \rm g = 0.1\; \rm kg`.
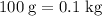• Mass of the second ball:
  `400\; \rm g = 0.4 \; \rm kg`.

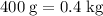The two balls stick to each other after the collision. In other words, this collision is a perfectly inelastic collision. Kinetic energy will not be conserved. The velocity of the two balls after the collision can only be found using the conservation of momentum.

Assume that the system of the two balls is isolated. Thus, the sum of the momentum of the two balls will stay the same before and after the collision.

The momentum of an object of mass
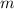`m` and velocity
`v` is:
`p = m \cdot v`.

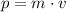Momentum of the two balls before collision:

• First ball:
  `p = m \cdot v = 0.1\; \rm kg * 100\; \rm m \cdot s^(-1) = 10\; \rm kg \cdot m \cdot s^(-1)`.
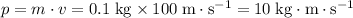• Second ball:
  `p = m \cdot v = 0.4\; \rm kg * 50\; \rm m \cdot s^(-1) = 20\; \rm kg \cdot m \cdot s^(-1)`.
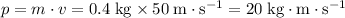• Sum:
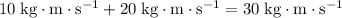  `10\; \rm kg \cdot m \cdot s^(-1) + 20 \; \rm kg \cdot m \cdot s^(-1) = 30 \; \rm kg \cdot m \cdot s^(-1)` given that the two balls are moving in the same direction.

Based on the assumptions, the sum of the momentum of the two balls after collision should also be
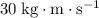`30\; \rm kg \cdot m \cdot s^(-1)`. The mass of the two balls, combined, is
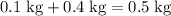`0.1\; \rm kg + 0.4\; \rm kg = 0.5\; \rm kg`. Let the velocity of the two balls after the collision
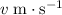`v\; \rm m \cdot s^(-1)`. (There's only one velocity because the collision had sticked the two balls to each other.)

• Momentum after the collision from
  `p = m \cdot v`:
  `(0.5\, v)\; \rm kg \cdot m \cdot s^{-1`.
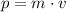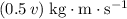• Momentum after the collision from the conservation of momentum:
  `30\; \rm kg \cdot m \cdot s^(-1)`.

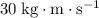These two values are supposed to describe the same quantity: the sum of the momentum of the two balls after the collision. They should be equal to each other. That gives the equation about
`v`:

`0.5\, v = 30`.

`v = 60`.

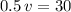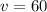In other words, the velocity of the two balls right after the collision should be
`60\; \rm m \cdot s^(-1)`.

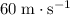Kinetic Energy

The kinetic energy of an object of mass
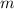`m` and velocity
`v` is
`\displaystyle (1)/(2)\, m \cdot v^(2)`.

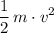Kinetic energy before the collision:

• First ball:
  `\displaystyle (1)/(2) \, m \cdot v^2 = (1)/(2)* 0.1\; \rm kg * \left(100\; \rm m \cdot s^(-1)\right)^(2) = 500\; \rm J`.
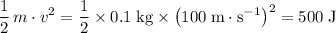• Second ball:
  `\displaystyle (1)/(2) \, m \cdot v^2 = (1)/(2)* 0.4\; \rm kg * \left(50\; \rm m \cdot s^(-1)\right)^(2) = 500\; \rm J`.
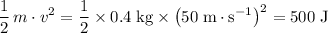• Sum:
  `500\; \rm J + 500\; \rm J = 1000\; \rm J`.

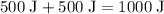The two balls stick to each other after the collision. Therefore, consider them as a single object when calculating the sum of their kinetic energies.

• Mass of the two balls, combined:
  `0.5\; \rm kg`.
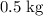• Velocity of the two balls right after the collision:
  `60\; \rm m\cdot s^(-1)`.

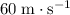Sum of the kinetic energies of the two balls right after the collision:

`\displaystyle (1)/(2) \, m \cdot v^(2) = (1)/(2)* 0.5\; \rm kg * \left(60\; \rm m \cdot s^(-1)\right)^2 = 900\; \rm J`.

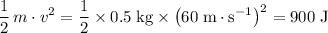Therefore,
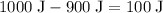`1000\; \rm J - 900\; \rm J = 100\; \rm J` of kinetic energy would be lost during this collision.